How to intuitively understand the relationship between equation, matrix, and space?

Linear algebra is the foundation of Machine Learning, Deep Learning, Optimization, etc. As is taught universally, we always start off in linear algebra from equation representations, and then we dive into spaces. Equation, matrix, and space are mirrors to each other, and their relationships help us understand linear algebra intuitively. This article is noted with my own intuitive understanding and aims to put every piece of the puzzle into one picture. Let’s dive in!

Set off with equation problems

Linear algebra is designed to solve equations. All equations can be represented by Matrix*Vector. One geometric interpretation for equations can be: Each row in equations is a constraint in X-Y-Z space and they all can form a feasible space inside the X-Y-Z space. However, it is not the space we are talking about here. We are talking about the column space. Here comes an interesting fact: Matrix*Vector = Combinations of Columns. The coefficient matrix can be expressed as 3 vectors in a 3-dimension space. The problem is then converted into “Can we find a linear combination of these 3 column vectors to form a new vector b?”.

Examples of linear combination in a 2-dimension space

We can stop here or we can push further. Plotting all linear combinations of these 3 column vectors, we can get a space (the dimension may not be 3! We will talk about it later.) Thus, the problem is actually asking about whether we can find the b vector in this space.

How to solve equations? Elimination!

As is often the case, we normally apply permutation, scalar multiplication, and subtraction to solve equations. All of those techniques can be mirrored by matrix multiplication (Matrix * Matrix). To understand Matrix*Matrix, let’s start with Vector*Matrix. Similar to Matrix*Vector’s representing combinations of columns, Vector*Matrix is the linear combination of rows. Try the second row in U matrix: -2 represents -2*row 1, 1 represents 1*row 2 (exactly how we eliminate in equations!), and then we successfully gain the result of row 2 in A’.

There are 2 types of matrixes that are used – elimination matrix and permutation matrix. The example above touches on the elimination matrix. Here is one example of the permutation matrix.

As for space interpretation, columns spaces are changed after row transformation. However, the idea behind the problem is the same.

Dive into the solutions of A’X=0

Starting with the solutions of A’X=0 instead pf jumping into A’X=b’ can help us build a deeper understanding of what we get after elimination and how we can find the solution space.

- Look closer to what’s left after elimination

Have you ever thought about the philosophy behind equation eliminations? Normally we would think of it as a way to reduce the number of variables in equations. But elimination can also be put as a way to reduce redundant information in equations. If 2 equations are redundant, say x+2y+3z=1 and 2x+4y+yz=2, only one of them contributes to forming the constraints. Thus, after elimination we are able to see the number of effective constraints. Moreover, it is reflected as the rank property in the matrix, and the number of independent columns in the column space.

- Solution Space

Now we are going to solve A’X=0! The example I give is a special example where there are no redundant constraints/no dependent columns/full rank, and where A is a square matrix. Therefore, the solution is merely a zero vector. To generalize, let’s try different shapes and different ranks of A’.

Whether A’X=0 has multiple solutions depends only on the relationship between rank and n. The intuition behind this is only when rank=n all columns we have are independent. No non-zero linear combination of independent vectors can produce 0. In the sense of equations, rank<n means that we do not have enough effective constraints thus multiple solutions are possible.

Multiple solutions form a solution space (nullspace). How can we represent this space? To form a k-dimension space, we need to find k independent vectors so the dimension of the solution space is crucial. After determining the dimension of the solution space, what’s left is only to find k specific solutions. The dimension of the solution space is exactly the number of dependent variables (ones that are constraint-free in equations!), which is (n-rank).

Dive further into the solutions of A’X=b’

Now we’ve seen the solution pattern in A’X=0, the solution space of A’X=b is similar but a little bit more complex. We only care about the relationship between rank and n in A’X=0, but now m is also included. Why is that? Here’s an example:

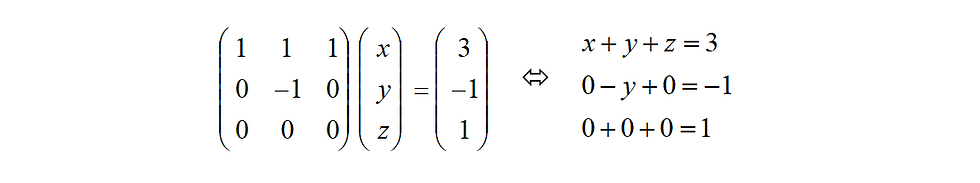
Zero combinations of any value of (x,y,z) can only produce 0, which results in possible insolvability in A’X=b.

The intuition behind it is based on effective dimensions which are equivalent to effective constraints. Though the dimension is 3, the effective dimension is 2 since all columns have 0 value on the 3rd dimension. It also indicates that the column space of rank 2 can at most represent 2-dimension vectors. And yes, you might notice that the number of effective dimensions is exactly the number of independent variables. They are the same thing but provide different perspectives.

In a nutshell, if rank<m and the values of redundant dimensions in b’ are not 0, the equations are not solvable.

Though it seems to be complex, there are patterns behind it.

• rank and m => redundant dimensions => solvable or not

• rank and n => dependent variables => unique or multiple solutions

Finally, we are able to solve the last puzzle – find the solution space for A’X=b’ when there are multiple solutions. Since we know how to form the space in A’X=0, the solution space for A’X=b’ is as simple as “one specific solution in A’X=b’ + solutions in A’X=0”.

By far, we are able to project the problem of equations into a geometric problem, and solve it using knowledge in spaces. Hope you will find this article useful.